最”主浔的打算用于å‘ç”µçš„æ ¸èšå˜ååº”æ˜¯è¿™æ ·çš„ï¼š
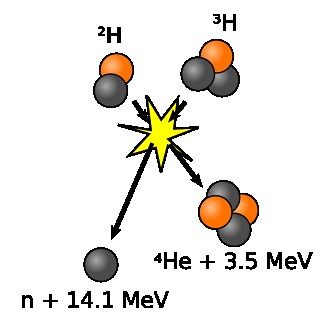
这就是氘氚èšå˜ã€‚上é¢çš„两个å‚与å应的原åæ ¸ï¼Œä¹Ÿå°±æ˜¯ç‡ƒæ–™ï¼Œæ˜¯æ°˜å’Œæ°šï¼Œä»–ä»¬æ˜¯æ°¢åŽŸåçš„åŒä½ç´ 。我们已ç»çŸ¥é“氢原åæ ¸å°±æ˜¯ä¸€ä¸ªè´¨å没有ä¸å,而氘(D)原 åæ ¸ç”±ä¸€ä¸ªè´¨å和一个ä¸å组æˆï¼Œæ°šï¼ˆT)包括一个质å和两个ä¸å。这个å应的结果是一个氦原åæ ¸ï¼ˆä¹Ÿå¯ä»¥è¯´æ˜¯è¢«å‰¥ç¦»äº†ä¸¤ä¸ªç”µå的氦离å)和一个ä¸å,用公 å¼è¡¨ç¤ºï¼š
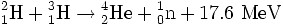
æ£å¦‚å‰é¢è®²è¿‡çš„裂å˜å应,两边质é‡ä¸åŒï¼Œå¯¼è‡´å³è¾¹å‡ºçŽ°äº†å¤šä½™çš„ 17.6MeV 的能é‡ï¼Œä½œä¸ºå应生æˆç‰©çš„动能。第一个图更直观的显示了动能的分é…,氦离å得到了3.5MeV,而ä¸å得到了14.1MeVã€‚èŽ·å¾—è¿™æ ·çš„åŠ¨èƒ½ï¼Œå®ƒä»¬çš„é€Ÿåº¦ 在æ¯ç§’一万公里以上。如果粒å的密度ä¸æ˜¯å¾ˆä½Žï¼Œäººä»¬ä¸€èˆ¬æŠŠè¿™æ ·çš„高速è¿åŠ¨ç§°ä¸ºï¼Œçˆ†ç‚¸ã€‚
下é¢æ˜¯å‡ 个常”觔的èšå˜å应:
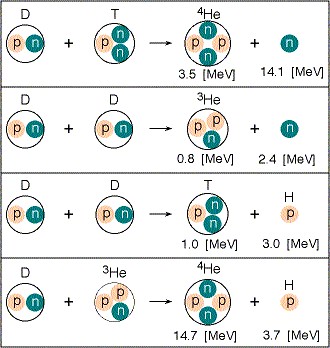
图ä¸è¿™å››ä¸ªå应å¼ä¸æˆ‘们å¯ä»¥çœ‹åˆ°ç¬¬ä¸€ä¸ªå’Œç¬¬å››ä¸ªäº§ç”Ÿçš„能é‡äº§å‡ºæœ€é«˜ã€‚注æ„第四个的å应的燃料是氘和”æ°¦3″, æ°¦3æ£æ˜¯æˆ‘国打算登月去寻找的èšå˜åŽŸæ–™ã€‚åŽé¢æˆ‘们将会说说氦3,现在还是回到第一个,也就是氘氚èšå˜ã€‚
我们首先看到这个èšå˜å应获得的能é‡æ¯”å‰æ–‡è¯´çš„é“€235裂å˜èƒ½é‡æ•ˆçŽ‡é«˜å¾ˆå¤šã€‚é“€235裂å˜ä¸ï¼Œ236ä¸ªæ ¸åå‚与å应åªå¾—到200MeVå·¦å³çš„能é‡ï¼Œè€Œè¿™ 里5ä¸ªæ ¸å就得到了17.6MeV,也就是说å•ä½è´¨é‡çš„æ ¸ç‡ƒæ–™ï¼Œèšå˜å¾—到的能é‡æ˜¯è£‚å˜çš„3å€å·¦å³ã€‚这就是为什么氢弹的å¨åŠ›è¿œå¤§äºŽåŽŸå弹。实际上氢弹用的也 是这个å应方程。这个效率高到什么程度呢,一个百万åƒç“¦çš„ç«åŠ›å‘电站,æ¯å¹´æ¶ˆè€—的煤是210万å¨ï¼›å¦‚果这个å‘电厂是裂å˜æ ¸ç”µç«™ï¼Œå®ƒéœ€è¦30å¨çš„æ ¸ç‡ƒæ–™ã€‚å¯ å¦‚æžœå®ƒæ˜¯æ ¸èšå˜å‘电厂,燃料åªéœ€è¦600 公斤。
å†æ¥çœ‹çœ‹ç‡ƒæ–™æ¥æºã€‚氘广泛å˜åœ¨äºŽæ°´é‡Œï¼ˆæ°˜å’Œæ°§åŽŸå组æˆçš„水就是é‡æ°´ï¼‰ï¼Œæ¯ 6700个(也有说法是5000个)”æ£å¸¸”氢原åä¸å°±æœ‰ä¸€ä¸ªæ˜¯æ°˜ï¼Œä¸€å‡æµ·æ°´ä¸åŒ…å«çš„氘所能释放的能é‡ç›¸å½“于300å‡æ±½æ²¹ã€‚æµ·æ°´ä¸æ‰€åŒ…å«çš„氘,在人类想象 力的范围内ä¸å¯èƒ½ç”¨å®Œã€‚而且从海水ä¸æ炼氘是容易的,1987年出版的书说1克氘的æˆæœ¬æ˜¯1美元,而2002å¹´çš„ä¸€ç¯‡æ–‡ç« åˆ™è¯´1公斤氘æ‰éœ€è¦300美元, 看æ¥è¶Šæ¥è¶Šä¾¿å®œã€‚相比之下1å…¬æ–¤æµ“ç¼©é“€çš„ä»·æ ¼æ˜¯12000美元。
è‡ªç„¶ç•Œå‡ ä¹Žæ²¡æœ‰å¤©ç„¶æ°šï¼Œå› ä¸ºæ°šå…·æœ‰æ”¾å°„æ€§ä¼šè¡°å˜ï¼ŒåŠè¡°æœŸå¤§çº¦æ˜¯åå‡ å¹´ã€‚åˆ¶å¤‡æ°šçš„æœ€å¸¸ç”¨åŠžæ³•æ˜¯è®©ä¸å跟锂å应:
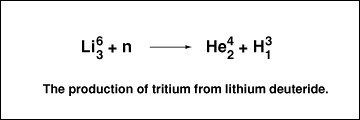
或者跟锂的å¦ä¸€ä¸ªåŒä½ç´ 也å¯ä»¥ã€‚实际上氢弹æ£æ˜¯è¿™ä¹ˆåšçš„。锂金属åŒæ ·ä¾¿å®œè€Œä¸°å¯Œï¼Œ1987å¹´ç¾Žå›½çš„ä»·æ ¼æ˜¯æ¯å…¬æ–¤åªè¦20ç¾Žå…ƒã€‚è€Œä¸”æŒ‰ç…§è¿™ä¸ªä»·æ ¼ï¼Œç¾Žå›½å¯ ä»¥è‡³å°‘æä¾›500万å¨ã€‚ä¸å›½çš„é”‚å‚¨å¤‡æ€Žä¹ˆæ ·å‘¢ï¼Ÿä¸å›½çš„锂储è—å 世界总é‡ä¸€åŠä»¥ä¸Šã€‚陆地储è—的锂至少å¯ä»¥ä¾›åšç‡ƒæ–™3万年,如果海里的也算上则是3000万 年。
按1987å¹´çš„ä»·æ ¼ï¼Œä¸–ç•Œæ¶ˆè´¹è€…å¹³å‡èŠ±è´¹åœ¨1G(10^9)焦耳电能上的钱是20ç¾Žå…ƒã€‚è€Œå¦‚æžœé‡‡ç”¨æ ¸èšå˜ï¼Œå‡è®¾èšå˜äº§ç”Ÿçš„能 é‡åªæœ‰1/3被实际利用的情况下,1G焦耳所需è¦çš„燃料(氘和锂)的花费åªæœ‰ä¸åˆ°0.004美元。æ¢å¥è¯è¯´èšå˜ç‡ƒæ–™çš„ä»·æ ¼å‡ ä¹Žå°±æ˜¯å¯ä»¥å¿½ç•¥çš„。说起æ¥åœ°çƒ 上的氘还是早期宇宙大爆炸åŽé•¿è¾¾ä¸€ç™¾ä¸‡å¹´çš„èšå˜å应没全没用完剩下的。信上å¸çš„人很å¯èƒ½ä¼šå–œæ¬¢è¿™ä¸ªäº‹å®žï¼Œé€ 物主盖好房å之åŽè¿˜å‰©ä¸‹ä¸€ç‚¹é’±ï¼Œå°±çœ‹åå™ä»¬æœ‰æ²¡ 有本事å–用了。
å¯æƒœèšå˜å‘电就好比90年代末在ä¸å›½çŽ©è®¡ç®—机游æˆï¼Œè™½ç„¶æ¸¸æˆè½¯ä»¶æœ¬èº«éƒ½æ˜¯ç›—版基本ä¸ç”¨èŠ±é’±ï¼Œä½†æ˜¯ç”µè„‘çš„ä»·æ ¼å¯ä¸ä¾¿å®œã€‚鱼倒是有的是,但是很难渔,而且鱼竿什么的巨贵。
两个原åæ ¸è¦æƒ³èšå˜ï¼Œä»–们必须é 的足够近。这就决定了两个æ£å¸¸åŽŸå之间是ä¸å¯èƒ½å‘生èšå˜çš„ï¼Œå› ä¸ºä»–ä»¬æ‰€å¸¦çš„ç”µå互相排斥的很厉害。所以第一æ¥å¿…须把电å 剥离(这一æ¥æ¯”较容易åšåˆ°ï¼‰ï¼Œå˜æˆçº¯åŽŸåæ ¸ï¼Œä¹Ÿå°±æ˜¯ç¦»å的状æ€ã€‚但是两个离å都带æ£ç”µï¼Œä»–们也是互相排斥,我们知é“电ç£æ–¥åŠ›å比于è·ç¦»ï¼Œè·ç¦»è¶‹è¿‘äºŽæ— ç©· å°ï¼Œæ–¥åŠ›å°±è¶‹è¿‘äºŽæ— ç©·å¤§ï¼Œå¦‚æžœè¿™ä¹ˆè¯´çš„è¯æ ¹æœ¬ä¸å¯èƒ½”蚔了。好在当è·ç¦»è¿‘到一定程度,原åæ ¸ä¹‹é—´ä¼šæ„Ÿå—到强相互作用的å¸å¼•åŠ›ï¼å¸å¼•åŠ›å’Œç”µç£æ–¥åŠ›ä¹‹é—´å…±åŒ 起作用的结果就是下é¢è¿™ä¸ªåŠ¿èƒ½æ›²çº¿ï¼š
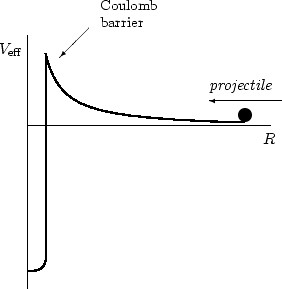
曲线的最高点称为库仑å±éšœã€‚想åƒè¿™æ˜¯ä¸€åº§å°å±±ï¼Œä½ è¦æ»šåŠ¨ä¸€ä¸ªçƒï¼Œè®©è¿™ä¸ªçƒè¶Šè¿‡å°å±±ã€‚显然çƒçš„动能越大它爬得越高,在我们日常生活的这个ç»å…¸ä¸–界,åªæœ‰å®ƒ 的动能大于库仑å±éšœï¼Œçƒæ‰èƒ½è¶Šè¿‡è¿™åº§å±±ã€‚这时候å‘生在原å尺度的第三个怪异的事实出现了:哪怕入射粒å的动能å°äºŽåº“仑å±éšœï¼Œå®ƒä¹Ÿå¯èƒ½ç¿»è¿‡å±±åŽ» ï¼è¿™ç§çŽ°è±¡å«åš”é‡å隧é“效应”,å¯ä»¥ç”¨ä¸‹å›¾æ¥æ绘:
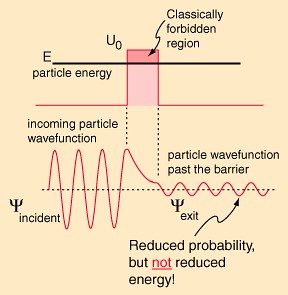
注æ„这里说的是å¯èƒ½æ€§ï¼Œæ˜¯è¯´å˜åœ¨ä¸€å®šçš„å‡ çŽ‡ï¼Œè€Œä¸”åŠ¨èƒ½ä¸ŽåŠ¿èƒ½å±è”½çš„å·®è·è¶Šå¤§ï¼Œè¿™ä¸ªå‡ 率就越å°ã€‚隧é“效应实在是个一个éžå¸¸å¥‡ç‰¹çš„现象,有点åƒä¼ 说ä¸çš„穿墙 术。ä¸è¿‡å®ƒå¹¶ä¸ç¥žç§˜ï¼šä¸€ä¸ªå¤§ä¸‰çš„物ç†ç³»æœ¬ç§‘生就知é“æ€Žä¹ˆç²¾ç¡®è®¡ç®—ç©¿å¢™å‡ çŽ‡ï¼Œè€Œä¸”å®ƒè¿˜æœ‰å¹¿æ³›åº”ç”¨ï¼Œæ¯”å¦‚è¯´éš§é“扫æ显微镜。有时候我想生活ä¸äººå…¶å®žä¹Ÿå˜åœ¨ä¸ä¸º é›¶çš„å‡ çŽ‡ç©¿å¢™è€Œè¿‡ï¼Œæ— éžå°±æ˜¯å…‹æœç”µç£ç›¸äº’作用的势能å£åž’,åªä¸è¿‡è¿™ä¸ªå‡ çŽ‡æ— æ¯”æ— æ¯”çš„æ— æ¯”å°è€Œå·²ã€‚
但ä¸è®ºå¦‚何,è¦æƒ³è®©èšå˜å应å‘ç”Ÿçš„å‡ çŽ‡å¤§åˆ°å¯ä»¥æŽ¥å—的程度,必须让氘和氚离å以æžé«˜çš„速度碰撞。下é¢è¿™å¼ 图显示了两个粒å一对一碰撞的è¯ï¼Œå„ç§ä¸åŒèšå˜å应å‘ç”Ÿçš„å‡ çŽ‡ç›¸å¯¹å¤§å°ï¼Œè·Ÿè¿™ä¸ªå…¥å°„ç²’å的动能之间的关系:
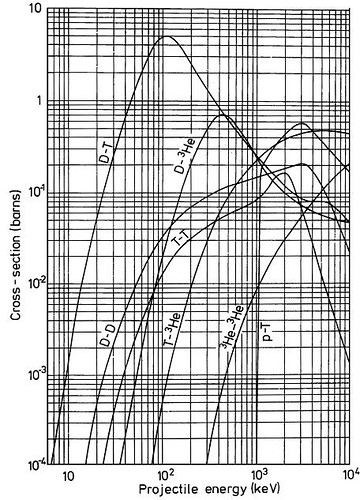
ä»Žè¿™å¼ å›¾å¯ä»¥çœ‹å‡ºåœ¨å…¥å°„动能且太”高的情况下,氘氚èšå˜å‘ç”Ÿæœ€å®¹æ˜“ã€‚æœ‰äº†è¿™å¼ å›¾æˆ‘ä»¬å°±å¯ä»¥ç²¾ç¡®è®¡ç®—å¦‚æžœä½ æŠŠä¸€å¤§å †æ°˜ç¦»åå’Œä¸€å¤§å †æ°šç¦»å放在一起,让他 们相互碰撞的è¯ï¼Œå应率是多少。å¯ä»¥æƒ³è±¡è¦æ±‚这些粒å都高速è¿åŠ¨ï¼Œè€Œç‰©ç†å¦å®¶å®šä¹‰çš„温度就是粒åçš„å¹³å‡åŠ¨èƒ½ï¼Œä¹Ÿå¯ä»¥ç´¢æ€§å°±ç”¨èƒ½é‡æ¥æ ‡è®°æ¸©åº¦ã€‚(韩乔生显然 对平å‡åŠ¨èƒ½å¦æœ‰å®šä¹‰ï¼Œå«åš”çƒåº¦”。 “今天沈阳的温度是11度,湿度是70%,çƒåº¦æ˜¯99%,呆会能达到100%。。。现在çƒåº¦è¾¾åˆ°äº†200%” – 摘自《韩大嘴è¯å½•ã€‹ï¼‰æ¸©åº¦æ˜¯å†³å®šæ€§çš„,这就是为什么èšå˜ä¹Ÿå«”çƒæ ¸å应”,也æ£æ˜¯å› ä¸ºè¿™ä¸ªåŽŸå› çˆ†ç‚¸æ°¢å¼¹éœ€è¦å…ˆå¼•çˆ†åŽŸåå¼¹æ¥æ供足够的高温。
å应率当然也跟离å数的密度有关,密度越高,å‘生的碰撞就越多,也就越容易å‘生å应。实际上å应率 R = n_D*n_T*<σV>。n_D å’Œ n_T 是氘和氚的密度,而<σV>完全由这些离åçš„å¹³å‡åŠ¨èƒ½ï¼Œä¹Ÿå°±æ˜¯æ°”体的温度,决定,如下图
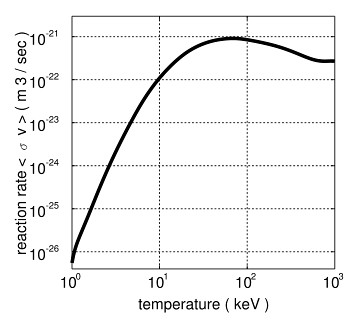
å¯è§æ°˜æ°šèšå˜çš„å应率在温度是100keV(1keVçš„å¹³å‡åŠ¨èƒ½å·®ä¸å¤šå¯¹åº”温度是1100万摄æ°åº¦ï¼‰å·¦å³çš„时候达到最高。å†ç»“åˆR = n_d*n_t*<σV>这个公å¼ï¼Œæˆ‘们å¯ä»¥å¾—出结论,è¦æƒ³æ高èšå˜çš„å应率,一方é¢è¦é«˜æ¸©ï¼Œå¦‚果温度ä¸å¤Ÿé«˜ï¼Œé‚£ä¹ˆå¯†åº¦å°±å¿…须高 – 比如说åƒå¤ªé˜³æ ¸å¿ƒå¯†åº¦é‚£ä¹ˆé«˜ã€‚
太阳能æ£æ˜¯æ¥è‡ªäºŽå…¶æ ¸å¿ƒå‘生的èšå˜å应,其过程差ä¸å¤šæ˜¯è¿™æ ·çš„:
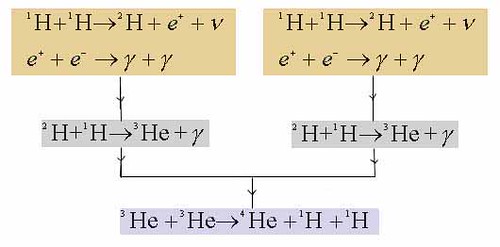
需è¦æ到并éžæ‰€æœ‰æ’æ˜Ÿéƒ½æŒ‰è¿™å‡ ä¸ªæ–¹ç¨‹ååº”ã€‚æ•´ä¸ªå¤ªé˜³çš„ç»“æž„æ˜¯è¿™æ ·çš„ï¼š
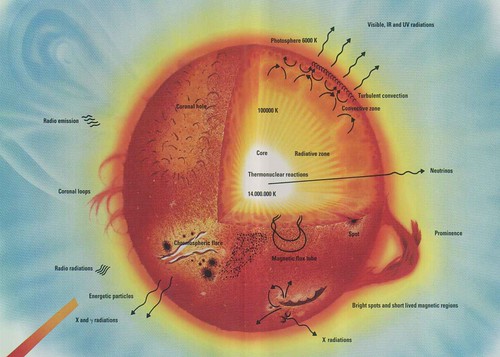
å…¶æ ¸å¿ƒæ¸©åº¦åœ¨1500万度左å³ã€‚这个温度在å应率曲线上并ä¸ç®—é«˜ï¼Œä½†æ˜¯å¤ªé˜³æ ¸å¿ƒå› ä¸ºè‡ªèº«å¼•åŠ›åŽ‹è¿«çš„åŽŸå› ï¼Œç²’å密度éžå¸¸é«˜ã€‚碰撞次数多了,就算å•æ¬¡ç¢°æ’žå‘生ååº”çš„å‡ çŽ‡ä½Žä¹Ÿæ²¡é—®é¢˜ï¼Œè¿™å°±å¥½æ¯”è¯´æœ‰äº›äººæœ¬æ¥å“è´¨ä¸é”™è´ªæ±¡çš„å‡ çŽ‡å¾ˆä½Žï¼Œä½†æ˜¯å¦‚æžœå‘¨å›´è¯±æƒ‘å¤ªå¤šçš„è¯å°±éš¾ä¿ä¸æ¹¿éž‹äº†ã€‚
有的情况是诱惑的多少,有的情况则是诱惑的大å°ã€‚在地çƒä¸Šæž”äººé€ å¤ªé˜³”第一æ¡å°±æ˜¯å¿…é¡»é™ä½Žå¯†åº¦ ,å¦åˆ™é«˜çƒåŠ 高密度必然爆炸就æˆäº†æ°¢å¼¹äº†ã€‚首先必须把实验装置ä¸çš„空气完全抽走,然åŽå†æ”¾å…¥æžå°‘é‡çš„氘氚气体,å†æŠŠå®ƒä»¬åŠ çƒå应。比如在一个体积是100 立方米的托克马克ä¸ï¼Œæ°˜æ°šæ°”体的总质é‡åªæœ‰0.01克。
密度这么低,这就è¦æ±‚实验的温度è¦æžé«˜ï¼Œæ‰˜å…‹é©¬å…‹ä¸æ°˜æ°šçš„温度è¦è¾¾åˆ°ä¸€äº¿ ç”šè‡³ä¸¤äº¿åº¦ï¼Œæ¯”å¤ªé˜³é«˜å¾—å¤šã€‚å› æ¤éœ€è¦æžå¤šçš„能é‡æ¥åŠ çƒç‚¹ç«ã€‚早在1929年,人们刚刚æ„识到çƒæ ¸èšå˜å¯ä»¥ç”¨ä½œèƒ½æºçš„时候,è‹è”æŸå®˜å‘˜æ›¾ç»è®¸è¯ºæŠŠåˆ—å®æ ¼å‹’市 一å°æ—¶çš„全部电力输出共给一个科å¦å®¶è®©ä»–åšå®žéªŒï¼Œè¢«ä»–明智地拒ç»äº†ã€‚今天æ供这些çƒé‡ç»™æ‰˜å…‹é©¬å…‹ç‚¹ç«å·²ç»å¯ä»¥å®žçŽ°äº†ï¼Œç®€å•è¯´æ˜¯åˆ©ç”¨æ¿€å…‰ï¼Œæˆ–è€…ä½Žé¢‘æ··æ‚ æ³¢ã€‚ï¼ˆä¸è¿‡è¦åŠ 到更高的温度,åƒçŽ°ä»£ç²’ååŠ é€Ÿå™¨é‚£æ ·ï¼Œæœ‰æ—¶å€™ä»ç„¶ä¼šå¨èƒé™„è¿‘åŸŽå¸‚çš„ç”¨ç”µã€‚æ¯”å¦‚è¥¿æ¬§æ ¸åä¸å¿ƒé™„近的城市曾ç»è¦æ±‚他们冬天少åšå‡ 次实验,好让有 电居民å–暖。)
低密度没问题,高温点ç«ä¹Ÿæ²¡é—®é¢˜ã€‚问题是怎么维æŒè¿™ä¸ªæ¸©åº¦ã€‚这就是托克马克的全部难点所在ï¼æˆ‘们先按下ä¸è¡¨ã€‚
从上é¢çš„讨论å¯ä»¥çŸ¥é“ï¼Œè®©æ ¸èšå˜å‘生,最关键的æ¡ä»¶æ˜¯é«˜æ¸©ã€‚那么”å†·æ ¸èšå˜”åˆæ˜¯æ€Žä¹ˆå›žäº‹å‘¢ï¼Ÿæ¸©åº¦ä¸çªå‡ºï¼Œå¯†åº¦ä¸çªå‡ºï¼Œä»€ä¹ˆçªå‡ºå‘¢ï¼Ÿå³ä½¿æ˜¯é‡å隧é“效应å…许,å应率也ç»å¯¹ä¸è¶…过10çš„è´Ÿ70次方ï¼éš¾é“å应率曲线错了么?有机会的è¯æˆ‘们å¯èƒ½ä¼šè®¨è®ºè¿™ä¸ªé—®é¢˜ã€‚
在全é¢ä»‹ç»æ‰˜å…‹é©¬å…‹ä¹‹å‰ï¼Œè¿˜æœ‰ä¸€ä¸ªå¾ˆæœ‰æ„æ€çš„é—®é¢˜ã€‚æˆ‘ä»¬åœ¨è¿™ä¸€ç« çœ‹åˆ°æ°˜æ°šèšå˜æ˜¯”最容易”å‘生的èšå˜å应。氘氚èšå˜è¦æ±‚的温度最低,而且原ææ–™è¿˜æ— æ¯”ä¾¿å®œï¼Œé‚£ä¹ˆä¸ºä»€ä¹ˆä¼šæœ‰äººå¯¹æ°¦3这么感兴趣呢?
(这ç§å†™æ³•å¤ªç´¯ï¼Œä¸‹ä¸€ç« çš„å†…å®¹è¿˜åœ¨é¢„ç ”é˜¶æ®µï¼Œéœ€è¦å¤šä¸€ç‚¹æ—¶é—´ï¼‰